| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 11.1 | Exercise 11.2 | Exercise 11.3 |
| Exercise 11.4 | Exercise 11.5 | |
Chapter 11 Algebra
Embark on the foundational journey into a transformative branch of mathematics with the solutions for Chapter 11: Algebra. This chapter marks a significant conceptual leap from arithmetic, introducing the powerful idea of using symbols, most commonly letters from the alphabet, to represent unknown or varying numerical quantities. Algebra provides a unique language and a set of tools essential for expressing mathematical relationships, solving complex problems, and building models of the world around us. Mastering these initial concepts is absolutely crucial, as algebra forms the bedrock upon which much of higher mathematics, science, engineering, and economics rests.
The provided solutions meticulously guide students through the essential building blocks of this fascinating subject:
- Understanding the core difference between variables and constants.
- Learning the art of constructing algebraic expressions.
- Applying these expressions to describe patterns and real-world scenarios.
- Grasping the definition and significance of an equation.
- Developing initial strategies for finding the solution to simple equations.
At the heart of algebra lies the concept of a variable. The solutions clearly explain that a variable, often denoted by letters like $x$, $y$, $n$, or $t$, is essentially a placeholder for a number whose value is either unknown or can change depending on the context. Think of it as a container that can hold different numerical values at different times. This is fundamentally different from a constant, which is a fixed numerical value that never changes, such as 5, -3, or $\pi$. Understanding this distinction is the first vital step into algebraic thinking.
Building upon variables and constants, the solutions demonstrate how to form algebraic expressions. These are meaningful combinations of variables, constants, and arithmetic operations (addition +, subtraction -, multiplication ×, division ÷). The process often involves translating simple verbal statements into concise symbolic form. For instance:
- "The sum of a number $n$ and 7" translates to the expression $n + 7$.
- "3 less than a number $y$" becomes $y - 3$.
- "The product of 6 and $x$" is written as $6 \times x$ or, more commonly in algebra, simply $6x$.
- "A number $z$ divided by 10" can be expressed as $z \div 10$ or $\frac{z}{10}$.
A particularly insightful application covered in the solutions is the use of expressions to define rules for patterns, such as those found in sequences of shapes made from matchsticks. If the first shape uses 3 matchsticks, the second 5, the third 7, the solutions guide students to see the pattern (adding 2 each time) and potentially derive a general rule, like $2n + 1$, where $n$ is the shape number, to find the number of matchsticks for *any* shape in the sequence. Furthermore, the utility of expressions in established formulas, like the perimeter of a rectangle $P = 2(l+b)$ (where $l$ and $b$ are variables representing length and breadth), is reinforced, showing algebra's role in generalizing geometric concepts.
The chapter then transitions to the crucial concept of an equation. Unlike an expression, which simply represents a value, an equation is a mathematical statement asserting that two expressions are equal. It always contains an equals sign (=). A typical example presented is $x + 3 = 10$. The solutions emphasize this key difference: $x+3$ is an expression, while $x+3=10$ is an equation, a declaration that the value represented by $x+3$ must be precisely 10.
A significant portion of the solutions is dedicated to the process of finding the solution of an equation. The solution is the specific numerical value of the variable that makes the equation a true statement. For introductory purposes, the primary method demonstrated is often trial and error (or inspection). Students are guided to substitute different plausible values for the variable into the equation and check if the equality holds true. For $x + 3 = 10$:
- Try $x=5$: Is $5 + 3 = 10$? No, $8 \ne 10$.
- Try $x=6$: Is $6 + 3 = 10$? No, $9 \ne 10$.
- Try $x=7$: Is $7 + 3 = 10$? Yes, $10 = 10$.
Therefore, $x=7$ is the solution. While effective for very simple equations, the solutions subtly prepare students for the eventual need for more systematic methods (like inverse operations, though perhaps not formally named yet) by illustrating the goal: finding the *unique* value that balances the equation.
By engaging with these Chapter 11 solutions, students will develop essential comfort and fluency with the symbolic language of algebra. This includes interpreting variables, constructing and manipulating expressions, and understanding the fundamental concept of solving equations. This initial grounding is indispensable, paving the way for success in virtually all subsequent mathematical and scientific studies where algebraic reasoning is ubiquitous.
Exercise 11.1
Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
(a) A pattern of letter T as

(b) A pattern of letter Z as

(c) A pattern of letter U as
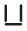
(d) A pattern of letter V as

(e) A pattern of letter E as
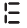
(f) A pattern of letter S as
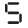
(g) A pattern of letter A as
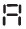
Answer:
To Find:
The rule (using a variable) for the number of matchsticks required to make patterns of the given letters.
Let $n$ be the variable representing the number of letters formed in the pattern.
Solution:
(a) Pattern of letter T
The image shows one letter T requires 2 matchsticks.
For a pattern of $n$ letters T, the number of matchsticks required would be $n$ times the matchsticks for one T.
Number of matchsticks = $2 \times n$
The rule is $2n$.
(b) Pattern of letter Z
The image shows one letter Z requires 3 matchsticks.
For a pattern of $n$ letters Z, the number of matchsticks required would be $n$ times the matchsticks for one Z.
Number of matchsticks = $3 \times n$
The rule is $3n$.
(c) Pattern of letter U
The image shows one letter U requires 3 matchsticks.
For a pattern of $n$ letters U, the number of matchsticks required would be $n$ times the matchsticks for one U.
Number of matchsticks = $3 \times n$
The rule is $3n$.
(d) Pattern of letter V
The image shows one letter V requires 2 matchsticks.
For a pattern of $n$ letters V, the number of matchsticks required would be $n$ times the matchsticks for one V.
Number of matchsticks = $2 \times n$
The rule is $2n$.
(e) Pattern of letter E
The image shows one letter E requires 5 matchsticks.
For a pattern of $n$ letters E, the number of matchsticks required would be $n$ times the matchsticks for one E.
Number of matchsticks = $5 \times n$
The rule is $5n$.
(f) Pattern of letter S
The image shows one letter S requires 5 matchsticks.
For a pattern of $n$ letters S, the number of matchsticks required would be $n$ times the matchsticks for one S.
Number of matchsticks = $5 \times n$
The rule is $5n$.
(g) Pattern of letter A
The image shows one letter A requires 6 matchsticks.
For a pattern of $n$ letters A, the number of matchsticks required would be $n$ times the matchsticks for one A.
Number of matchsticks = $6 \times n$
The rule is $6n$.
Question 2. We already know the rule for the pattern of letters L, C and F. Some of the letters from Q.1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?
Answer:
Given:
The rules for patterns of letters L, C, and F are known. The rules derived in Question 1 for letters T, Z, U, V, E, S, and A.
Rule for L: A single letter L requires 2 matchsticks. For $n$ letters, the rule is $2n$.
Rule for C: A single letter C requires 3 matchsticks. For $n$ letters, the rule is $3n$.
Rule for F: A single letter F requires 4 matchsticks. For $n$ letters, the rule is $4n$.
To Find:
Which letters from Question 1 (T, Z, U, V, E, S, A) have the same rule as the letter L? Why?
Solution:
From Question 1, we found the following rules:
(a) Rule for T is $2n$.
(b) Rule for Z is $3n$.
(c) Rule for U is $3n$.
(d) Rule for V is $2n$.
(e) Rule for E is $5n$.
(f) Rule for S is $5n$.
(g) Rule for A is $6n$.
The rule for the pattern of letter L is $2n$ because each letter L requires 2 matchsticks.
Comparing this rule ($2n$) with the rules found in Question 1, we see that the letters T and V also have the rule $2n$.
Therefore, the letters from Question 1 that give the same rule as L are T and V.
Reason:
This happens because the number of matchsticks required to make one pattern of the letter L is 2, and similarly, the number of matchsticks required to make one pattern of the letter T is 2, and the number of matchsticks required to make one pattern of the letter V is also 2. Since the number of matchsticks required for each individual letter (L, T, V) is the same (which is 2), the rule for finding the total number of matchsticks for $n$ letters ($2 \times n$) is also the same.
Question 3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use n for the number of rows.)
Answer:
Given:
Number of cadets in one row = 5
The number of rows is represented by the variable $n$.
To Find:
The rule which gives the total number of cadets, given the number of rows ($n$).
Solution:
Let $n$ be the number of rows.
The number of cadets in each row is fixed at 5.
To find the total number of cadets, we multiply the number of cadets in one row by the total number of rows.
Total number of cadets = (Number of cadets in a row) $\times$ (Number of rows)
Total number of cadets = $5 \times n$
Therefore, the rule is $5n$.
Question 4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.)
Answer:
Given:
Number of mangoes in one box = 50
The number of boxes is represented by the variable $b$.
To Find:
The rule (expression) for the total number of mangoes in terms of the number of boxes ($b$).
Solution:
Let $b$ be the number of boxes.
Each box contains 50 mangoes.
To find the total number of mangoes, we multiply the number of mangoes in one box by the total number of boxes.
Total number of mangoes = (Number of mangoes in one box) $\times$ (Number of boxes)
Total number of mangoes = $50 \times b$
Therefore, the rule for the total number of mangoes is $50b$.
Question 5. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use s for the number of students.)
Answer:
Given:
Number of pencils distributed per student = 5
The number of students is represented by the variable $s$.
To Find:
The rule for the total number of pencils needed, given the number of students ($s$).
Solution:
Let $s$ be the number of students.
Each student receives 5 pencils.
To find the total number of pencils needed, we multiply the number of pencils given to one student by the total number of students.
Total number of pencils needed = (Number of pencils per student) $\times$ (Number of students)
Total number of pencils needed = $5 \times s$
Therefore, the rule for the number of pencils needed is $5s$.
Question 6. A bird flies 1 kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (Use t for flying time in minutes.)
Answer:
Given:
Speed of the bird = $1$ kilometer per minute.
Flying time = $t$ minutes.
To Express:
The distance covered by the bird in terms of its flying time $t$.
Solution:
The formula relating distance, speed, and time is:
Distance = Speed $\times$ Time
We are given the speed of the bird as $1$ km/minute and the time as $t$ minutes.
Substituting these values into the formula, we get:
Distance = $1$ km/minute $\times$ $t$ minutes
Distance = $t$ kilometers
So, the distance covered by the bird in $t$ minutes is $t$ kilometers.
We can express this relationship as:
$D = t$
where $D$ is the distance in kilometers and $t$ is the flying time in minutes.
Question 7. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots) with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows?
How many dots are there if there are 8 rows? If there are 10 rows?
Answer:
Given:
Number of dots Radha has in one row = 9.
To Find:
1. The total number of dots in the Rangoli for 'r' rows.
2. The total number of dots if there are 8 rows.
3. The total number of dots if there are 10 rows.
Solution:
Let 'r' be the number of rows and 'd' be the total number of dots.
We are given that the number of dots in one single row is 9.
The total number of dots will be the product of the number of dots in one row and the total number of rows.
So, Total number of dots = (Number of dots in one row) $\times$ (Number of rows)
$d = 9 \times r$
Therefore, the Rangoli will have $9r$ dots for r rows.
Number of dots for 8 rows:
Here, the number of rows is $r = 8$.
Using the rule derived above, we can find the total number of dots.
Total dots = $9r$
Total dots = $9 \times 8 = 72$
Hence, if there are 8 rows, there will be 72 dots.
Number of dots for 10 rows:
Here, the number of rows is $r = 10$.
Using the same rule:
Total dots = $9r$
Total dots = $9 \times 10 = 90$
Hence, if there are 10 rows, there will be 90 dots.
Question 8. Leela is Radha's younger sister. Leela is 4 years younger than Radha. Can you write Leela's age in terms of Radha's age? Take Radha's age to be x years.
Answer:
Given:
Radha's age = $x$ years.
Leela is 4 years younger than Radha.
To Find:
Leela's age in terms of Radha's age ($x$).
Solution:
We are given that Leela is 4 years younger than Radha. This means that Leela's age is Radha's age minus 4 years.
Let Leela's age be represented by $L$ years.
According to the information given:
Leela's age = Radha's age - 4
$L = x - 4$
... (i)
So, Leela's age can be expressed in terms of Radha's age ($x$) as $x - 4$ years.
Question 9. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is l, how many laddus did she make?
Answer:
Given:
Number of laddus remaining = $5$.
Number of laddus given away = $l$.
To Find:
The total number of laddus mother made.
Solution:
The total number of laddus mother made is the sum of the laddus she gave away and the laddus that are remaining.
Let the total number of laddus mother made be represented by $M$.
So, we can write the relationship as:
Total laddus made = Laddus given away + Laddus remaining
$M = l + 5$
... (i)
Thus, the total number of laddus mother made is $l + 5$.
Question 10. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?
Answer:
Given:
Number of oranges in a small box = $x$.
When a large box is emptied, the oranges fill two smaller boxes, and 10 oranges remain outside.
To Find:
The number of oranges in the larger box.
Solution:
Let $L$ be the number of oranges in the larger box.
According to the problem statement, when the oranges from the large box are transferred, they fill two smaller boxes completely.
The number of oranges in one small box is $x$.
So, the number of oranges in two smaller boxes is $2 \times x = 2x$.
After filling the two smaller boxes, there are still 10 oranges remaining outside.
This means the total number of oranges that were in the large box is the sum of the oranges in the two small boxes and the remaining oranges.
Number of oranges in the large box = (Number of oranges in two small boxes) + (Number of remaining oranges)
$L = 2x + 10$
... (i)
Therefore, the number of oranges in the larger box is $2x + 10$.
Question 11.

(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)

(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
Answer:
Solution:
Part (a): Matchstick pattern of squares
We observe the pattern of matchsticks forming squares (Fig 11.6). The squares are joined such that adjacent squares share a vertical matchstick.
Let $n$ be the number of squares and $M_s$ be the number of matchsticks used to form the pattern.
Let's list the number of matchsticks for the first few numbers of squares:
| Number of Squares (n) | Number of Matchsticks ($M_s$) |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 13 |
We observe that the number of matchsticks increases by 3 for each additional square.
Let's find a rule relating $M_s$ and $n$. We can see the pattern as one square requiring 4 sticks, and each subsequent square adding 3 sticks.
Number of matchsticks = (Matchsticks for first square) + (Number of additional squares) $\times$ (Matchsticks added per additional square)
$M_s = 4 + (n - 1) \times 3$
$M_s = 4 + 3n - 3$
$M_s = 3n + 1$
Alternatively, as per the hint, if we consider the pattern as $n$ shapes like 'C' followed by a vertical stick at the end:
Each 'C' requires 3 matchsticks. For $n$ squares, we can think of $n$ 'C' shapes using $3n$ sticks, plus one extra vertical stick at the very right end.
Total matchsticks = $3n + 1$
The rule that gives the number of matchsticks in terms of the number of squares is:
$$M_s = 3n + 1$$
Part (b): Matchstick pattern of triangles
We observe the pattern of matchsticks forming triangles (Fig 11.7). The triangles are joined such that adjacent triangles share a vertical matchstick.
Let $n$ be the number of triangles and $M_t$ be the number of matchsticks used to form the pattern.
Let's list the number of matchsticks for the first few numbers of triangles:
| Number of Triangles (n) | Number of Matchsticks ($M_t$) |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
We observe that the number of matchsticks increases by 2 for each additional triangle.
Let's find a rule relating $M_t$ and $n$. We can see the pattern as one triangle requiring 3 sticks, and each subsequent triangle adding 2 sticks.
Number of matchsticks = (Matchsticks for first triangle) + (Number of additional triangles) $\times$ (Matchsticks added per additional triangle)
$M_t = 3 + (n - 1) \times 2$
$M_t = 3 + 2n - 2$
$M_t = 2n + 1$
Alternatively, we can see the pattern as $n$ bases (horizontal sticks) and $n+1$ slanted sticks (vertical sticks). The bases are the $n$ horizontal sticks. For the slanted sticks, there is one on the left end, one on the right end, and $n-1$ shared vertical sticks in between.
Number of bases = $n$ sticks
Number of slanted sticks = $1 (\text{left}) + (n-1) (\text{shared}) + 1 (\text{right}) = n+1$ sticks
Total matchsticks = $n + (n+1) = 2n + 1$
The rule that gives the number of matchsticks in terms of the number of triangles is:
$$M_t = 2n + 1$$
Exercise 11.2
Question 1. The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
Answer:
Given:
The side length of an equilateral triangle is $l$.
To Express:
The perimeter of the equilateral triangle using $l$.
Solution:
An equilateral triangle is a triangle in which all three sides are equal in length.
The perimeter of any triangle is the sum of the lengths of its three sides.
In an equilateral triangle with side length $l$, all three sides have a length of $l$.
Perimeter = Side 1 + Side 2 + Side 3
Perimeter = $l + l + l$
Adding the three sides together, we get:
Perimeter = $3 \times l$
Perimeter = $3l$
Let $P$ represent the perimeter of the equilateral triangle.
$P = 3l$
Thus, the perimeter of the equilateral triangle with side length $l$ is $3l$.
Question 2. The side of a regular hexagon (Fig 11.10) is denoted by l.
Express the perimeter of the hexagon using l.
(Hint: A regular hexagon has all its six sides equal in length.)

Answer:
Given:
The side length of a regular hexagon is denoted by $l$.
To Express:
The perimeter of the regular hexagon using $l$.
Solution:
A regular hexagon is a polygon with six sides of equal length.
The perimeter of any polygon is the sum of the lengths of its sides.
Since a regular hexagon has six equal sides, and the length of each side is $l$, the perimeter is the sum of the lengths of all six sides.
Perimeter = Side 1 + Side 2 + Side 3 + Side 4 + Side 5 + Side 6
Perimeter = $l + l + l + l + l + l$
Perimeter = $6 \times l$
Let $P$ represent the perimeter of the regular hexagon.
$$P = 6l$$
Thus, the perimeter of a regular hexagon with side length $l$ is $6l$.
Question 3. A cube is a three-dimensional figure as shown in Fig 11.11. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.
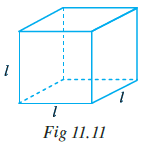
Answer:
Given:
The length of an edge of the cube is $l$.
A cube is a three-dimensional figure with 6 identical square faces.
To Find:
The formula for the total length of the edges of a cube.
Solution:
A cube has edges where its faces meet. Let's count the number of edges in a cube.
A cube has 4 edges on the bottom face, 4 edges on the top face, and 4 vertical edges connecting the corresponding corners of the top and bottom faces.
Total number of edges in a cube = $4 + 4 + 4 = 12$.
Since it is a cube, all edges are of equal length. The length of each edge is given as $l$.
To find the total length of the edges, we multiply the number of edges by the length of one edge.
Total length of edges = (Number of edges) $\times$ (Length of one edge)
Total length of edges = $12 \times l$
Let $L_{\text{total}}$ represent the total length of the edges of the cube.
$$L_{\text{total}} = 12l$$
Thus, the formula for the total length of the edges of a cube with edge length $l$ is $12l$.

Answer:
Given:
A circle with centre C.
AB is a diameter of the circle, passing through the centre C.
The radius of the circle is denoted by $r$.
The diameter of the circle is denoted by $d$.
To Express:
The diameter ($d$) in terms of the radius ($r$).
Solution:
The radius of a circle is the distance from the centre to any point on the circle.
In the given figure, C is the centre, and points A and B are on the circle.
The line segment AC is a radius of the circle, so its length is $r$.
AC = $r$
Similarly, the line segment CB is a radius of the circle, so its length is $r$.
CB = $r$
The diameter AB is a line segment passing through the centre C, with endpoints A and B on the circle. The length of the diameter AB is the sum of the lengths of AC and CB.
Diameter (d) = AC + CB
Diameter (d) = $r + r$
Diameter (d) = $2r$
So, the diameter of the circle ($d$) can be expressed in terms of its radius ($r$) as:
$$d = 2r$$
This means the diameter of a circle is twice its radius.
Question 5. To find sum of three numbers 14, 27 and 13, we can have two ways:
(a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54.
Thus, (14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on Whole Numbers, in a general way, by using variables a, b and c.
Answer:
Given:
The property of associativity of addition for three specific numbers 14, 27, and 13, which is $(14 + 27) + 13 = 14 + (27 + 13)$.
The property holds for any three numbers.
We are asked to use variables $a$, $b$, and $c$ to express this property in a general way.
To Express:
The associative property of addition using variables $a$, $b$, and $c$.
Solution:
The associative property of addition states that when three or more numbers are added, the sum is the same regardless of the grouping of the addends.
If we have three numbers, let's call them $a$, $b$, and $c$, the associative property of addition says that we can group them in two ways for addition without changing the result.
We can first add $a$ and $b$, and then add $c$ to the result. This is represented as $(a + b) + c$.
Alternatively, we can first add $b$ and $c$, and then add $a$ to the result. This is represented as $a + (b + c)$.
The associative property states that these two ways of grouping give the same sum.
Therefore, the general expression for the associative property of addition using variables $a$, $b$, and $c$ is:
$$(a + b) + c = a + (b + c)$$
This equation holds true for any values of the variables $a$, $b$, and $c$.
Exercise 11.3
Question 1. Make up as many expressions with numbers (no variables) as you can from three numbers 5, 7 and 8. Every number should be used not more than once. Use only addition, subtraction and multiplication.
(Hint: Three possible expressions are 5 + (8 – 7), 5 – (8 – 7), (5 × 8) + 7; make the other expressions.)
Answer:
Given:
The three numbers are 5, 7, and 8.
The allowed operations are addition (+), subtraction (-), and multiplication (×).
Each number must be used not more than once in every expression.
Solution:
We can create many different expressions by using the numbers 5, 7, and 8, and the operations of addition, subtraction, and multiplication. Each number must be used exactly once.
The three possible expressions given in the hint are:
$5 + (8 – 7)$
$5 – (8 – 7)$
$(5 \times 8) + 7$
Here is a list of several other expressions that can be formed:
Expressions using Addition and Subtraction:
1. $(5 + 7) - 8$
2. $8 - (5 + 7)$
3. $7 + (8 - 5)$
4. $(8 - 5) + 7$
5. $5 - (7 + 8)$
6. $(5 - 8) + 7$
Expressions using Multiplication and Addition:
7. $5 + (7 \times 8)$
8. $8 + (5 \times 7)$
9. $(5 + 7) \times 8$
10. $5 \times (7 + 8)$
11. $7 \times (5 + 8)$
12. $(8 + 5) \times 7$
Expressions using Multiplication and Subtraction:
13. $(5 \times 7) - 8$
14. $8 - (5 \times 7)$
15. $5 - (7 \times 8)$
16. $5 \times (8 - 7)$
17. $8 \times (7 - 5)$
18. $(8 - 7) \times 5$
Expression using only Multiplication:
19. $5 \times 7 \times 8$
Question 2. Which out of the following are expressions with numbers only?
(a) y + 3
(b) (7 × 20) – 8z
(c) 5 (21 – 7) + 7 × 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) (7 × 20) – (5 × 10) – 45 + p
Answer:
Given:
A list of expressions.
To Identify:
Expressions that contain numbers only (no variables).
Solution:
We need to examine each expression and determine if it contains any variables (like $x, y, z, n, p$, etc.). Expressions with numbers only will not have any variables.
(a) $y + 3$: This expression contains the variable $y$. Therefore, it is not an expression with numbers only.
(b) $(7 \times 20) - 8z$: This expression contains the variable $z$. Therefore, it is not an expression with numbers only.
(c) $5 (21 - 7) + 7 \times 2$: This expression contains only numbers (5, 21, 7, 7, 2) and mathematical operations (subtraction, multiplication, addition). There are no variables. Therefore, this is an expression with numbers only.
(d) $5$: This expression contains only a number (5). There are no variables. Therefore, this is an expression with numbers only.
(e) $3x$: This expression contains the variable $x$. Therefore, it is not an expression with numbers only.
(f) $5 - 5n$: This expression contains the variable $n$. Therefore, it is not an expression with numbers only.
(g) $(7 \times 20) - (5 \times 10) - 45 + p$: This expression contains the variable $p$. Therefore, it is not an expression with numbers only.
Based on the analysis, the expressions with numbers only are (c) and (d).
Question 3. Identify the operations (addition, subtraction, division, multiplication) in forming the following expressions and tell how the expressions have been formed.
(a) z + 1, z – 1, y + 17, y – 17
(b) 17y, $\frac{y}{17}$ , 5 z
(c) 2y + 17, 2y – 17
(d) 7 m, – 7 m + 3, – 7 m – 3
Answer:
Solution:
We will identify the operations used in each expression and describe how the expression is formed.
(a) $z + 1$, $z - 1$, $y + 17$, $y - 17$
- $z + 1$: The operation used is addition. This expression is formed by adding 1 to the variable $z$.
- $z - 1$: The operation used is subtraction. This expression is formed by subtracting 1 from the variable $z$.
- $y + 17$: The operation used is addition. This expression is formed by adding 17 to the variable $y$.
- $y - 17$: The operation used is subtraction. This expression is formed by subtracting 17 from the variable $y$.
(b) $17y$, $\frac{y}{17}$, $5z$
- $17y$: The operation used is multiplication. This expression is formed by multiplying the variable $y$ by 17.
- $\frac{y}{17}$: The operation used is division. This expression is formed by dividing the variable $y$ by 17.
- $5z$: The operation used is multiplication. This expression is formed by multiplying the variable $z$ by 5.
(c) $2y + 17$, $2y - 17$
- $2y + 17$: The operations used are multiplication and addition. This expression is formed by first multiplying the variable $y$ by 2, and then adding 17 to the result.
- $2y - 17$: The operations used are multiplication and subtraction. This expression is formed by first multiplying the variable $y$ by 2, and then subtracting 17 from the result.
(d) $7m$, $-7m + 3$, $-7m - 3$
- $7m$: The operation used is multiplication. This expression is formed by multiplying the variable $m$ by 7.
- $-7m + 3$: The operations used are multiplication and addition. This expression is formed by first multiplying the variable $m$ by $-7$, and then adding 3 to the result.
- $-7m - 3$: The operations used are multiplication and subtraction. This expression is formed by first multiplying the variable $m$ by $-7$, and then subtracting 3 from the result.
Question 4. Give expressions for the following cases.
(a) 7 added to p
(b) 7 subtracted from p
(c) p multiplied by 7
(d) p divided by 7
(e) 7 subtracted from – m
(f) – p multiplied by 5
(g) – p divided by 5
(h) p multiplied by – 5
Answer:
Solution:
We will write the expressions for each given case.
(a) 7 added to $p$:
This means we start with $p$ and add 7 to it.
Expression: $p + 7$
(b) 7 subtracted from $p$:
This means we start with $p$ and subtract 7 from it.
Expression: $p - 7$
(c) $p$ multiplied by 7:
This means we multiply $p$ by 7. In algebra, we usually write the number before the variable.
Expression: $7p$
(d) $p$ divided by 7:
This means we divide $p$ by 7. This can be written as a fraction.
Expression: $\frac{p}{7}$
(e) 7 subtracted from $-m$:
This means we start with $-m$ and subtract 7 from it.
Expression: $-m - 7$
(f) $-p$ multiplied by 5:
This means we multiply $-p$ by 5. The result will be negative.
Expression: $5 \times (-p) = -5p$
(g) $-p$ divided by 5:
This means we divide $-p$ by 5.
Expression: $\frac{-p}{5}$ or $-\frac{p}{5}$
(h) $p$ multiplied by $-5$:
This means we multiply $p$ by $-5$. The result will be negative.
Expression: $-5 \times p = -5p$
Question 5. Give expressions in the following cases.
(a) 11 added to 2m
(b) 11 subtracted from 2m
(c) 5 times y to which 3 is added
(d) 5 times y from which 3 is subtracted
(e) y is multiplied by – 8
(f) y is multiplied by – 8 and then 5 is added to the result
(g) y is multiplied by 5 and the result is subtracted from 16
(h) y is multiplied by – 5 and the result is added to 16.
Answer:
Solution:
We will write the algebraic expressions for each given case.
(a) 11 added to $2m$:
This means we take the quantity $2m$ and add 11 to it.
Expression: $2m + 11$
(b) 11 subtracted from $2m$:
This means we start with the quantity $2m$ and subtract 11 from it.
Expression: $2m - 11$
(c) 5 times $y$ to which 3 is added:
First, find 5 times $y$, which is $5 \times y = 5y$.
Then, add 3 to the result.
Expression: $5y + 3$
(d) 5 times $y$ from which 3 is subtracted:
First, find 5 times $y$, which is $5 \times y = 5y$.
Then, subtract 3 from the result.
Expression: $5y - 3$
(e) $y$ is multiplied by $-8$:
This means we multiply $y$ by $-8$. The number is usually written before the variable.
Expression: $-8 \times y = -8y$
(f) $y$ is multiplied by $-8$ and then 5 is added to the result:
First, multiply $y$ by $-8$, which gives $-8y$.
Then, add 5 to this result.
Expression: $-8y + 5$
(g) $y$ is multiplied by 5 and the result is subtracted from 16:
First, multiply $y$ by 5, which gives $5y$.
Then, subtract this result ($5y$) from 16.
Expression: $16 - 5y$
(h) $y$ is multiplied by $-5$ and the result is added to 16:
First, multiply $y$ by $-5$, which gives $-5y$.
Then, add this result ($-5y$) to 16.
Expression: $16 + (-5y) = 16 - 5y$
Question 6.
(a) Form expressions using t and 4. Use not more than one number operation. Every expression must have t in it.
(b) Form expressions using y, 2 and 7. Every expression must have y in it. Use only two number operations. These should be different.
Answer:
(a) Form expressions using t and 4. Use not more than one number operation. Every expression must have t in it.
Solution:
We are given the variable 't' and the number '4'. We can use the four basic arithmetic operations (addition, subtraction, multiplication, and division) to form the expressions. Since we can use not more than one operation, here are the possible expressions:
1. Using Addition: The expression is $t + 4$.
2. Using Subtraction: We can form two different expressions: $t - 4$ and $4 - t$.
3. Using Multiplication: The expression is $4 \times t$, which is commonly written as $4t$.
4. Using Division: We can form two different expressions: $\frac{t}{4}$ and $\frac{4}{t}$.
So, the expressions are: $t + 4$, $t - 4$, $4 - t$, $4t$, $\frac{t}{4}$, and $\frac{4}{t}$.
(b) Form expressions using y, 2 and 7. Every expression must have y in it. Use only two number operations. These should be different.
Solution:
We need to form expressions using the variable 'y' and the numbers '2' and '7'. Each expression must use two different operations.
Here are some of the many possible expressions:
1. Using Multiplication and Addition:
- $2y + 7$ (First multiply y by 2, then add 7)
- $7y + 2$ (First multiply y by 7, then add 2)
2. Using Multiplication and Subtraction:
- $2y - 7$ (First multiply y by 2, then subtract 7)
- $7y - 2$ (First multiply y by 7, then subtract 2)
- $7 - 2y$ (First multiply y by 2, then subtract the result from 7)
3. Using Division and Addition:
- $\frac{y}{2} + 7$ (First divide y by 2, then add 7)
- $\frac{y}{7} + 2$ (First divide y by 7, then add 2)
4. Using Division and Subtraction:
- $\frac{y}{2} - 7$ (First divide y by 2, then subtract 7)
- $7 - \frac{y}{2}$ (First divide y by 2, then subtract the result from 7)
5. Using brackets with different operations:
- $2(y + 7)$ (Addition and Multiplication)
- $7(y - 2)$ (Subtraction and Multiplication)
- $\frac{y+2}{7}$ (Addition and Division)
- $\frac{y-7}{2}$ (Subtraction and Division)
Exercise 11.4
Question 1. Answer the following:
(a) Take Sarita’s present age to be y years
(i) What will be her age 5 years from now?
(ii) What was her age 3 years back?
(iii) Sarita’s grandfather is 6 times her age. What is the age of her grandfather?
(iv) Grandmother is 2 years younger than grandfather. What is grandmother's age?
(v) Sarita’s father’s age is 5 years more than 3 times Sarita’s age. What is her father's age?
(b) The length of a rectangular hall is 4 meters less than 3 times the breadth of the hall. What is the length, if the breadth is b meters?
(c) A rectangular box has height h cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.
(d) Meena, Beena and Leena are climbing the steps to the hill top. Meena is at step s, Beena is 8 steps ahead and Leena 7 steps behind. Where are Beena and Meena? The total number of steps to the hill top is 10 less than 4 times what Meena has reached. Express the total number of steps using s.
(e) A bus travels at v km per hour. It is going from Daspur to Beespur. After the bus has travelled 5 hours, Beespur is still 20 km away. What is the distance from Daspur to Beespur? Express it using v.
Answer:
Solution:
(a) Sarita's age and related ages:
Given that Sarita’s present age is $y$ years.
(i) Age 5 years from now:
After 5 years, Sarita's age will be her current age plus 5 years.
Sarita's age 5 years from now = $y + 5$ years.
(ii) Age 3 years back:
3 years back, Sarita's age was her current age minus 3 years.
Sarita's age 3 years back = $y - 3$ years.
(iii) Grandfather's age:
Grandfather's age is 6 times Sarita's age.
Grandfather's age = $6 \times y = 6y$ years.
(iv) Grandmother's age:
Grandmother is 2 years younger than grandfather.
Grandmother's age = Grandfather's age - 2 = $6y - 2$ years.
(v) Sarita’s father’s age:
Sarita’s father’s age is 5 years more than 3 times Sarita’s age.
3 times Sarita's age = $3 \times y = 3y$ years.
Father's age = $3y + 5$ years.
(b) Length of a rectangular hall:
Given that the breadth of the hall is $b$ meters.
The length is 4 meters less than 3 times the breadth.
3 times the breadth = $3 \times b = 3b$ meters.
Length = $3b - 4$ meters.
(c) Dimensions of a rectangular box:
Given that the height of the box is $h$ cm.
Length is 5 times the height.
Length = $5 \times h = 5h$ cm.
Breadth is 10 cm less than the length.
Breadth = Length - 10 cm = $5h - 10$ cm.
(d) Steps on the hill top:
Given that Meena is at step $s$.
Beena is 8 steps ahead of Meena.
Beena is at step = $s + 8$.
Leena is 7 steps behind Meena.
Leena is at step = $s - 7$.
The total number of steps to the hill top is 10 less than 4 times what Meena has reached.
4 times what Meena has reached = $4 \times s = 4s$.
Total number of steps = $4s - 10$.
(e) Distance from Daspur to Beespur:
Given that the bus travels at $v$ km per hour.
Time travelled = 5 hours.
Distance covered by the bus in 5 hours = Speed $\times$ Time = $v \times 5 = 5v$ km.
After travelling for 5 hours, Beespur is still 20 km away.
The total distance from Daspur to Beespur is the distance covered by the bus plus the remaining distance.
Total distance from Daspur to Beespur = Distance covered + Remaining distance = $5v + 20$ km.
Question 2. Change the following statements using expressions into statements in ordinary language.
(For example, Given Salim scores r runs in a cricket match, Nalin scores (r + 15) runs. In ordinary language – Nalin scores 15 runs more than Salim.)
(a) A notebook costs ₹ p. A book costs ₹ 3 p.
(b) Tony puts q marbles on the table. He has 8 q marbles in his box.
(c) Our class has n students. The school has 20 n students.
(d) Jaggu is z years old. His uncle is 4 z years old and his aunt is (4z – 3) years old.
(e) In an arrangement of dots there are r rows. Each row contains 5 dots.
Answer:
Solution:
We will translate each statement containing an expression into ordinary language.
(a) A notebook costs $\textsf{₹}$ $p$. A book costs $\textsf{₹}$ $3p$.
In ordinary language: The cost of a book is 3 times the cost of a notebook.
(b) Tony puts $q$ marbles on the table. He has $8q$ marbles in his box.
In ordinary language: Tony has 8 times the number of marbles in his box as he puts on the table.
(c) Our class has $n$ students. The school has $20n$ students.
In ordinary language: The total number of students in the school is 20 times the number of students in our class.
(d) Jaggu is $z$ years old. His uncle is $4z$ years old and his aunt is $(4z - 3)$ years old.
In ordinary language: Jaggu's uncle is 4 times as old as Jaggu. His aunt is 3 years younger than his uncle (or 3 years less than 4 times Jaggu's age).
(e) In an arrangement of dots there are $r$ rows. Each row contains 5 dots.
In ordinary language: The arrangement has $r$ rows, and each row consists of 5 dots. The total number of dots is 5 times the number of rows.
Question 3.
(a) Given Munnu’s age to be x years, can you guess what (x – 2) may show?
(Hint: Think of Munnu’s younger brother.)
Can you guess what (x + 4) may show? What (3x + 7) may show?
(b) Given Sara’s age today to be y years. Think of her age in the future or in the past.
What will the following expression indicate? y + 7, y – 3, y + $4\frac{1}{2}$ , y – $2\frac{1}{2}$ .
(c) Given n students in the class like football, what may 2n show? What may $\frac{n}{2}$ show? (Hint: Think of games other than football).
Answer:
(a) Given Munnu’s age to be x years, can you guess what (x – 2) may show? Can you guess what (x + 4) may show? What (3x + 7) may show?
Solution:
Given that Munnu's current age is x years.
1. The expression (x – 2) represents 2 years less than Munnu's current age. This could show the age of Munnu's younger sibling who is 2 years younger than him, or it could represent Munnu's own age 2 years ago.
2. The expression (x + 4) represents 4 years more than Munnu's current age. This could show the age of Munnu's older sibling who is 4 years older than him, or it could represent Munnu's own age 4 years in the future.
3. The expression (3x + 7) represents 7 more than 3 times Munnu's age. This could show the age of an older family member, such as his father or uncle. For example, if Munnu is 10 years old (x=10), then 3x + 7 would be $3 \times 10 + 7 = 37$, which is a plausible age for a father.
(b) Given Sara’s age today to be y years. Think of her age in the future or in the past. What will the following expression indicate? y + 7, y – 3, y + $4\frac{1}{2}$ , y – $2\frac{1}{2}$.
Solution:
Given that Sara's current age is y years.
1. The expression y + 7 indicates Sara's age 7 years from now, i.e., her age in the future.
2. The expression y – 3 indicates Sara's age 3 years ago, i.e., her age in the past.
3. The expression y + $4\frac{1}{2}$ indicates Sara's age after four and a half years, i.e., her age in the future.
4. The expression y – $2\frac{1}{2}$ indicates Sara's age two and a half years ago, i.e., her age in the past.
(c) Given n students in the class like football, what may 2n show? What may $\frac{n}{2}$ show?
Solution:
Given that the number of students in the class who like football is n.
1. The expression 2n represents twice the number of students who like football. This could show the number of students who like a different game, for example, cricket, if the number of students who like cricket is double the number of students who like football.
2. The expression $\frac{n}{2}$ represents half the number of students who like football. This could show the number of students who like another game, for example, basketball, if the number of students who like basketball is half the number of students who like football.
Exercise 11.5
Question 1. State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t – 7) > 5
(c) $\frac{4}{2}$ = 2
(d) (7 × 3) – 19 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 × 5) – (12 × 4)
(j) 7 = (11 × 2) + p
(k) 20 = 5y
(l) $\frac{3q}{2}$ < 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
Answer:
Solution:
An equation is a statement that two expressions are equal. It must contain an equality sign (=). An equation with a variable contains one or more variables.
(a) $17 = x + 7$
This is an equation with a variable because it has an equality sign and contains the variable $x$. The variable is $x$.
(b) $(t – 7) > 5$
This is not an equation because it has an inequality sign ($>$) instead of an equality sign. It is an inequality.
(c) $\frac{4}{2} = 2$
This is not an equation with a variable because although it has an equality sign, it does not contain any variable. It is a numerical statement.
(d) $(7 \times 3) – 19 = 8$
This is not an equation with a variable because although it has an equality sign, it does not contain any variable. It is a numerical statement.
(e) $5 \times 4 – 8 = 2x$
This is an equation with a variable because it has an equality sign and contains the variable $x$. The variable is $x$.
(f) $x – 2 = 0$
This is an equation with a variable because it has an equality sign and contains the variable $x$. The variable is $x$.
(g) $2m < 30$
This is not an equation because it has an inequality sign ($<$) instead of an equality sign. It is an inequality.
(h) $2n + 1 = 11$
This is an equation with a variable because it has an equality sign and contains the variable $n$. The variable is $n$.
(i) $7 = (11 \times 5) – (12 \times 4)$
This is not an equation with a variable because although it has an equality sign, it does not contain any variable. It is a numerical statement.
(j) $7 = (11 \times 2) + p$
This is an equation with a variable because it has an equality sign and contains the variable $p$. The variable is $p$.
(k) $20 = 5y$
This is an equation with a variable because it has an equality sign and contains the variable $y$. The variable is $y$.
(l) $\frac{3q}{2} < 5$
This is not an equation because it has an inequality sign ($<$) instead of an equality sign. It is an inequality.
(m) $z + 12 > 24$
This is not an equation because it has an inequality sign ($>$) instead of an equality sign. It is an inequality.
(n) $20 – (10 – 5) = 3 \times 5$
This is not an equation with a variable because although it has an equality sign, it does not contain any variable. It is a numerical statement.
(o) $7 – x = 5$
This is an equation with a variable because it has an equality sign and contains the variable $x$. The variable is $x$.
Question 2. Complete the entries in the third column of the table.
| S.No. | Equation | Value of variable | Equation satisfied Yes/No |
|---|---|---|---|
| (a) | $10y = 80$ | $y = 10$ | |
| (b) | $10y = 80$ | $y = 8$ | |
| (c) | $10y = 80$ | $y = 5$ | |
| (d) | $4l = 20$ | $l = 20$ | |
| (e) | $4l = 20$ | $l = 80$ | |
| (f) | $4l = 20$ | $l = 5$ | |
| (g) | $b + 5 = 9$ | $b = 5$ | |
| (h) | $b + 5 = 9$ | $b = 9$ | |
| (i) | $b + 5 = 9$ | $b = 4$ | |
| (j) | $h – 8 = 5$ | $h = 13$ | |
| (k) | $h – 8 = 5$ | $h = 8$ | |
| (l) | $h – 8 = 5$ | $h = 0$ | |
| (m) | $p + 3 = 1$ | $p = 3$ | |
| (n) | $p + 3 = 1$ | $p = 1$ | |
| (o) | $p + 3 = 1$ | $p = 0$ | |
| (p) | $p + 3 = 1$ | $p = – 1$ | |
| (q) | $p + 3 = 1$ | $p = – 2$ |
Answer:
Solution:
We substitute the given value of the variable into the equation and check if the left-hand side (LHS) is equal to the right-hand side (RHS).
| S.No. | Equation | Value of variable | LHS | RHS | Equation satisfied Yes/No |
| (a) | $10y = 80$ | $y = 10$ | $10 \times 10 = 100$ | 80 | No |
| (b) | $10y = 80$ | $y = 8$ | $10 \times 8 = 80$ | 80 | Yes |
| (c) | $10y = 80$ | $y = 5$ | $10 \times 5 = 50$ | 80 | No |
| (d) | $4l = 20$ | $l = 20$ | $4 \times 20 = 80$ | 20 | No |
| (e) | $4l = 20$ | $l = 80$ | $4 \times 80 = 320$ | 20 | No |
| (f) | $4l = 20$ | $l = 5$ | $4 \times 5 = 20$ | 20 | Yes |
| (g) | $b + 5 = 9$ | $b = 5$ | $5 + 5 = 10$ | 9 | No |
| (h) | $b + 5 = 9$ | $b = 9$ | $9 + 5 = 14$ | 9 | No |
| (i) | $b + 5 = 9$ | $b = 4$ | $4 + 5 = 9$ | 9 | Yes |
| (j) | $h – 8 = 5$ | $h = 13$ | $13 - 8 = 5$ | 5 | Yes |
| (k) | $h – 8 = 5$ | $h = 8$ | $8 - 8 = 0$ | 5 | No |
| (l) | $h – 8 = 5$ | $h = 0$ | $0 - 8 = -8$ | 5 | No |
| (m) | $p + 3 = 1$ | $p = 3$ | $3 + 3 = 6$ | 1 | No |
| (n) | $p + 3 = 1$ | $p = 1$ | $1 + 3 = 4$ | 1 | No |
| (o) | $p + 3 = 1$ | $p = 0$ | $0 + 3 = 3$ | 1 | No |
| (p) | $p + 3 = 1$ | $p = – 1$ | $-1 + 3 = 2$ | 1 | No |
| (q) | $p + 3 = 1$ | $p = – 2$ | $-2 + 3 = 1$ | 1 | Yes |
Question 3. Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation.
(a) 5m = 60
(b) n + 12 = 20
(c) p – 5 = 5
(d) $\frac{q}{2}$ = 7
(e) r – 4 = 0
(f) x + 4 = 2
(10, 5, 12, 15)
(12, 8, 20, 0)
(0, 10, 5 – 5)
(7, 2, 10, 14)
(4, – 4, 8, 0)
(– 2, 0, 2, 4)
Answer:
Solution:
We will test each given value by substituting it into the equation to see if it satisfies the equation (makes the LHS equal to the RHS).
(a) $5m = 60$; Given values: 10, 5, 12, 15
Check $m = 10$:
LHS = $5 \times 10 = 50$. RHS = 60.
Since $50 \neq 60$, $m = 10$ does not satisfy the equation.
Check $m = 5$:
LHS = $5 \times 5 = 25$. RHS = 60.
Since $25 \neq 60$, $m = 5$ does not satisfy the equation.
Check $m = 12$:
LHS = $5 \times 12 = 60$. RHS = 60.
Since $60 = 60$, $m = 12$ satisfies the equation.
Check $m = 15$:
LHS = $5 \times 15 = 75$. RHS = 60.
Since $75 \neq 60$, $m = 15$ does not satisfy the equation.
The solution is $m = 12$. The other values (10, 5, 15) do not satisfy the equation.
(b) $n + 12 = 20$; Given values: 12, 8, 20, 0
Check $n = 12$:
LHS = $12 + 12 = 24$. RHS = 20.
Since $24 \neq 20$, $n = 12$ does not satisfy the equation.
Check $n = 8$:
LHS = $8 + 12 = 20$. RHS = 20.
Since $20 = 20$, $n = 8$ satisfies the equation.
Check $n = 20$:
LHS = $20 + 12 = 32$. RHS = 20.
Since $32 \neq 20$, $n = 20$ does not satisfy the equation.
Check $n = 0$:
LHS = $0 + 12 = 12$. RHS = 20.
Since $12 \neq 20$, $n = 0$ does not satisfy the equation.
The solution is $n = 8$. The other values (12, 20, 0) do not satisfy the equation.
(c) $p – 5 = 5$; Given values: 0, 10, 5, – 5
Check $p = 0$:
LHS = $0 - 5 = -5$. RHS = 5.
Since $-5 \neq 5$, $p = 0$ does not satisfy the equation.
Check $p = 10$:
LHS = $10 - 5 = 5$. RHS = 5.
Since $5 = 5$, $p = 10$ satisfies the equation.
Check $p = 5$:
LHS = $5 - 5 = 0$. RHS = 5.
Since $0 \neq 5$, $p = 5$ does not satisfy the equation.
Check $p = -5$:
LHS = $-5 - 5 = -10$. RHS = 5.
Since $-10 \neq 5$, $p = -5$ does not satisfy the equation.
The solution is $p = 10$. The other values (0, 5, -5) do not satisfy the equation.
(d) $\frac{q}{2} = 7$; Given values: 7, 2, 10, 14
Check $q = 7$:
LHS = $\frac{7}{2} = 3.5$. RHS = 7.
Since $3.5 \neq 7$, $q = 7$ does not satisfy the equation.
Check $q = 2$:
LHS = $\frac{2}{2} = 1$. RHS = 7.
Since $1 \neq 7$, $q = 2$ does not satisfy the equation.
Check $q = 10$:
LHS = $\frac{10}{2} = 5$. RHS = 7.
Since $5 \neq 7$, $q = 10$ does not satisfy the equation.
Check $q = 14$:
LHS = $\frac{14}{2} = 7$. RHS = 7.
Since $7 = 7$, $q = 14$ satisfies the equation.
The solution is $q = 14$. The other values (7, 2, 10) do not satisfy the equation.
(e) $r – 4 = 0$; Given values: 4, – 4, 8, 0
Check $r = 4$:
LHS = $4 - 4 = 0$. RHS = 0.
Since $0 = 0$, $r = 4$ satisfies the equation.
Check $r = -4$:
LHS = $-4 - 4 = -8$. RHS = 0.
Since $-8 \neq 0$, $r = -4$ does not satisfy the equation.
Check $r = 8$:
LHS = $8 - 4 = 4$. RHS = 0.
Since $4 \neq 0$, $r = 8$ does not satisfy the equation.
Check $r = 0$:
LHS = $0 - 4 = -4$. RHS = 0.
Since $-4 \neq 0$, $r = 0$ does not satisfy the equation.
The solution is $r = 4$. The other values (-4, 8, 0) do not satisfy the equation.
(f) $x + 4 = 2$; Given values: – 2, 0, 2, 4
Check $x = -2$:
LHS = $-2 + 4 = 2$. RHS = 2.
Since $2 = 2$, $x = -2$ satisfies the equation.
Check $x = 0$:
LHS = $0 + 4 = 4$. RHS = 2.
Since $4 \neq 2$, $x = 0$ does not satisfy the equation.
Check $x = 2$:
LHS = $2 + 4 = 6$. RHS = 2.
Since $6 \neq 2$, $x = 2$ does not satisfy the equation.
Check $x = 4$:
LHS = $4 + 4 = 8$. RHS = 2.
Since $8 \neq 2$, $x = 4$ does not satisfy the equation.
The solution is $x = -2$. The other values (0, 2, 4) do not satisfy the equation.
Question 4.
(a) Complete the table and by inspection of the table find the solution to the equation m + 10 = 16.
| $m$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | __ | __ | __ |
| $m + 10$ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ |
(b) Complete the table and by inspection of the table, find the solution to the equation 5t = 35.
| $t$ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | __ | __ | __ | __ | __ |
| $5t$ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ |
(c) Complete the table and find the solution of the equation $\frac{z}{3}$ =4 using the table.
| $z$ | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | __ | __ | __ | __ |
| $\frac{z}{3}$ | $2\frac{2}{3}$ | $3$ | $3\frac{1}{3}$ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ |
(d) Complete the table and find the solution to the equation m – 7 = 3.
| $m$ | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | __ | __ |
| $m - 7$ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ | __ |
Answer:
To Find:
To complete the given tables and find the solution to the equations by inspection.
Solution:
(a) Complete the table and by inspection of the table find the solution to the equation $m + 10 = 16$.
We need to find the value of $m+10$ for each given value of $m$. The completed table is as follows:
| $m$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| $m + 10$ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
By inspecting the table, we can see that when $m = 6$, the value of $m + 10$ is 16.
Therefore, the solution to the equation $m + 10 = 16$ is $m = 6$.
(b) Complete the table and by inspection of the table, find the solution to the equation $5t = 35$.
We need to find the value of $5t$ for each given value of $t$. The completed table is as follows:
| $t$ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| $5t$ | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
By inspecting the table, we observe that when $t = 7$, the value of $5t$ is 35.
Therefore, the solution to the equation $5t = 35$ is $t = 7$.
(c) Complete the table and find the solution of the equation $\frac{z}{3} = 4$ using the table.
We need to find the value of $\frac{z}{3}$ for each given value of $z$. The completed table is as follows:
| $z$ | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| $\frac{z}{3}$ | $2\frac{2}{3}$ | 3 | $3\frac{1}{3}$ | $3\frac{2}{3}$ | 4 | $4\frac{1}{3}$ | $4\frac{2}{3}$ | 5 | $5\frac{1}{3}$ | $5\frac{2}{3}$ | 6 | $6\frac{1}{3}$ | $6\frac{2}{3}$ |
By inspecting the table, we see that when $z = 12$, the value of $\frac{z}{3}$ is 4.
Therefore, the solution to the equation $\frac{z}{3} = 4$ is $z = 12$.
(d) Complete the table and find the solution to the equation $m – 7 = 3$.
We need to find the value of $m-7$ for each given value of $m$. The completed table is as follows:
| $m$ | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| $m - 7$ | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
By inspecting the table, we find that when $m = 10$, the value of $m - 7$ is 3.
Therefore, the solution to the equation $m - 7 = 3$ is $m = 10$.
Question 5. Solve the following riddles, you may yourself construct such riddles.
Who am I?
(i) Go round a square Counting every corner Thrice and no more! Add the count to me To get exactly thirty four!
(ii) For each day of the week Make an upcount from me If you make no mistake You will get twenty three!
(iii) I am a special number Take away from me a six! A whole cricket team You will still be able to fix!
(iv) Tell me who I am I shall give a pretty clue! You will get me back If you take me out of twenty two!
Answer:
Solution:
Let the unknown number be represented by a variable.
(i) Riddle:
A square has 4 corners. Counting every corner thrice means $3 \times 4 = 12$.
Let the unknown number be $N$.
Adding the count (12) to the number ($N$) gives 34.
This can be written as an equation:
$N + 12 = 34$
To find $N$, subtract 12 from both sides of the equation:
$N = 34 - 12$
$N = 22$
The number is 22.
(ii) Riddle:
There are 7 days in a week.
Let the unknown number be $N$.
Making an upcount from the number for each day of the week means adding 7 to the number.
The result is 23.
This can be written as an equation:
$N + 7 = 23$
To find $N$, subtract 7 from both sides of the equation:
$N = 23 - 7$
$N = 16$
The number is 16.
(iii) Riddle:
Let the unknown number be $N$.
Take away 6 from the number: $N - 6$.
A whole cricket team has 11 players.
The result is 11.
This can be written as an equation:
$N - 6 = 11$
To find $N$, add 6 to both sides of the equation:
$N = 11 + 6$
$N = 17$
The number is 17.
(iv) Riddle:
Let the unknown number be $N$.
Taking the number out of 22 means $22 - N$.
You will get the number back, meaning the result is $N$.
This can be written as an equation:
$22 - N = N$
To solve for $N$, add $N$ to both sides of the equation:
$22 = N + N$
$22 = 2N$
Divide both sides by 2:
$N = \frac{22}{2}$
$N = 11$
The number is 11.

